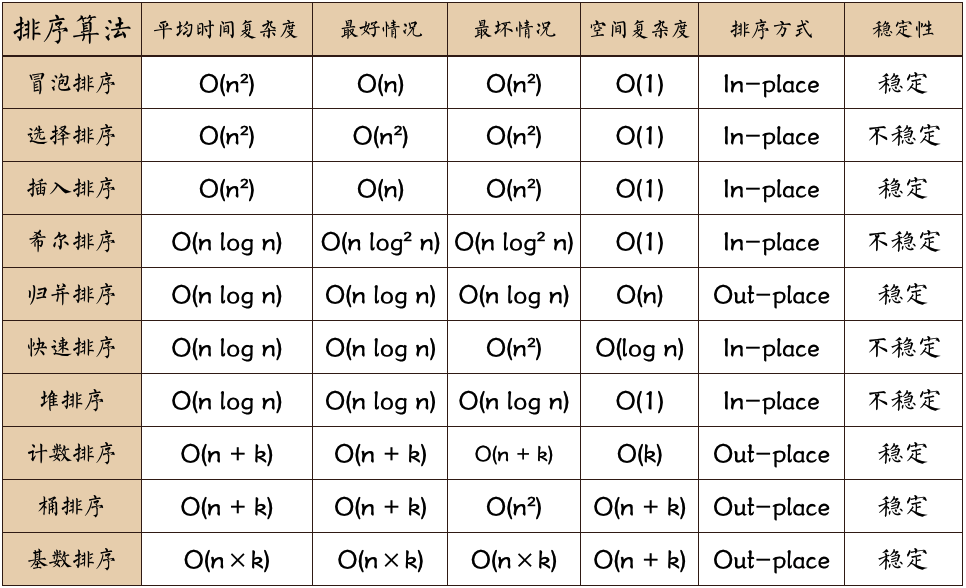
1. 概述
名词解释:
n:数据规模
k:“桶”的个数
In-place:占用常数内存,不占用额外内存
Out-place:占用额外内存
稳定性:排序后2个相等键值的顺序和排序之前它们的顺序相同
2. 目录
2.1 冒泡排序
2.2 选择排序
2.3 插入排序
2.4 归并排序
2.5 快速排序
为了方便说明,默认按从小到大排序,可参见算法可视化工具
3. 排序详情
3.1 冒泡排序
基本原理:
重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
排序步骤:
1.依次比较相邻的两个数,如果第一个比第二个小,不变;如果第一个比第二个大,调换顺序;一轮下来,最后一个是最大的数;
2.对除了最后一个之外的数重复第一步,直到只剩一个数。
图像展示:
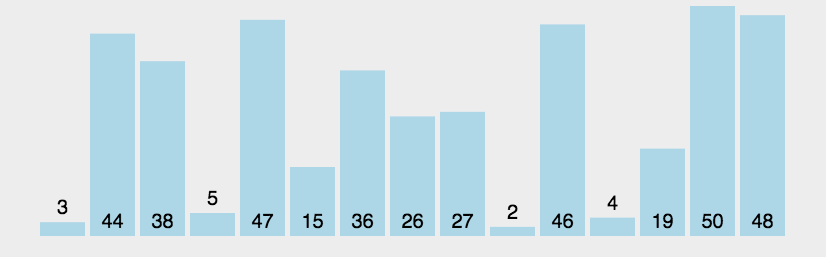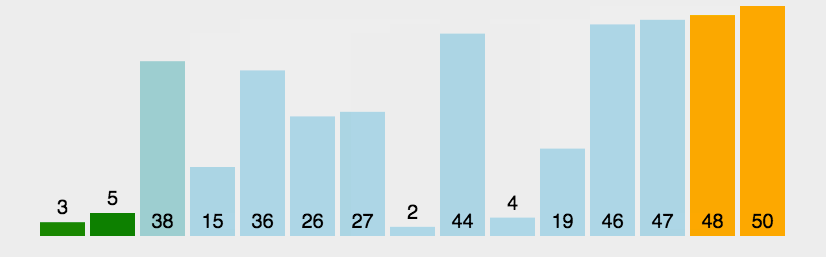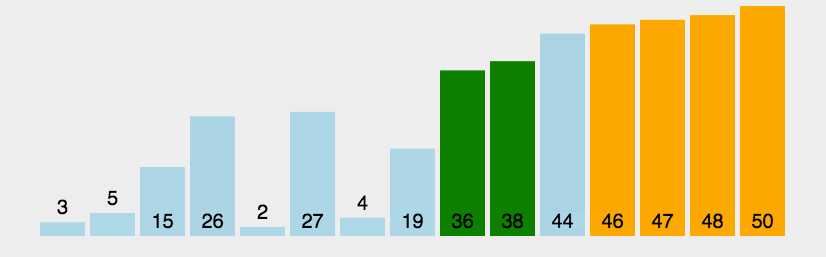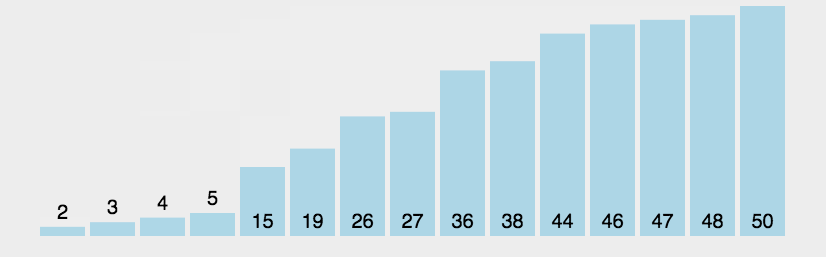
代码实现:
通用部分代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15var arr = []
// 交换数组中两个元素的位置
function swap(arr, a, b) {
var temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
// 生成随机数组
function generate(count, max) {
arr = [];
for (var i = 0; i < count; i++) {
arr.push(Math.round(Math.random() * max));
}
}
generate(100, 100);
冒泡排序代码:1
2
3
4
5
6
7
8
9
10
11function bubbleSort(arr) {
for (var i = 0; i < arr.length - 1; i++) {
for (var j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
}
}
}
return arr;
}
bubbleSort(arr);
3.2 选择排序
基本原理:
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
排序步骤:
1.遍历数组,找出最小的数,和第一个交换位置;
2.在剩下的数中,找出最二小的数,放在第二个;
3.依次类推,排出顺序。
图像展示:
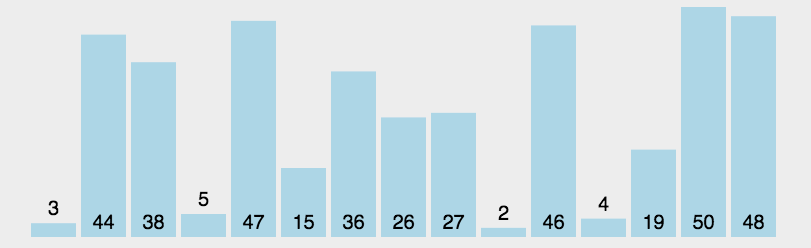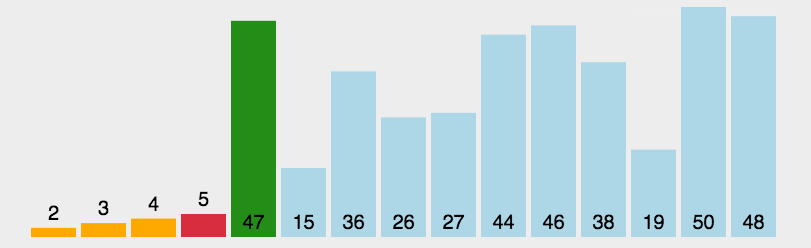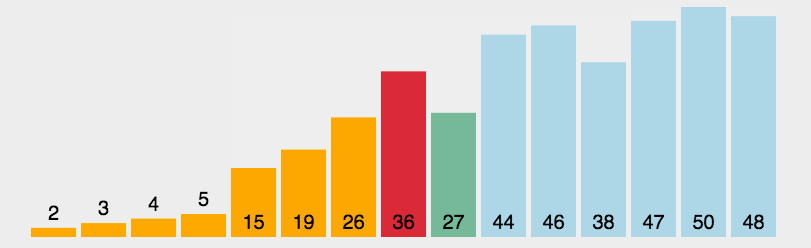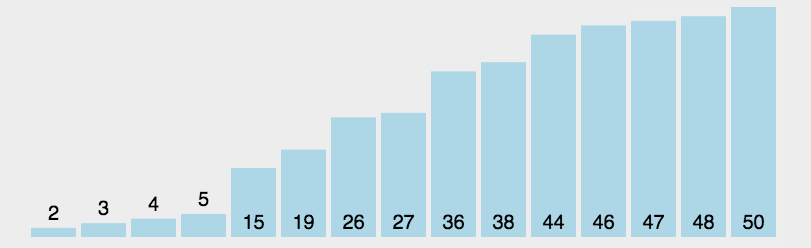
代码实现:
选择排序代码:1
2
3
4
5
6
7
8
9
10
11
12function selectSort(arr) {
for (var i = 0; i < arr.length-1; i++) {
var minIndex = i;
for (var j = i+1; j < arr.length; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
swap(arr, i, minIndex);
}
return arr;
}
3.3 插入排序
基本原理:
通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到 {\displaystyle O(1)} {\displaystyle O(1)}的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
排序步骤:
1.把数组分为[已排序]和[未排序]两部分,第一个数为[已排序],其余为[未排序];
2.从[未排序]抽出第一个数,和[已排序]部分比较,插入到合适的位置。
图像展示:
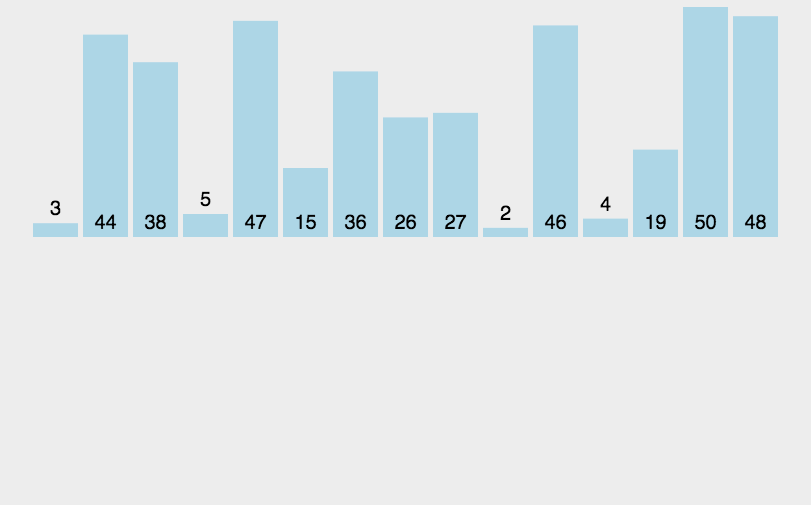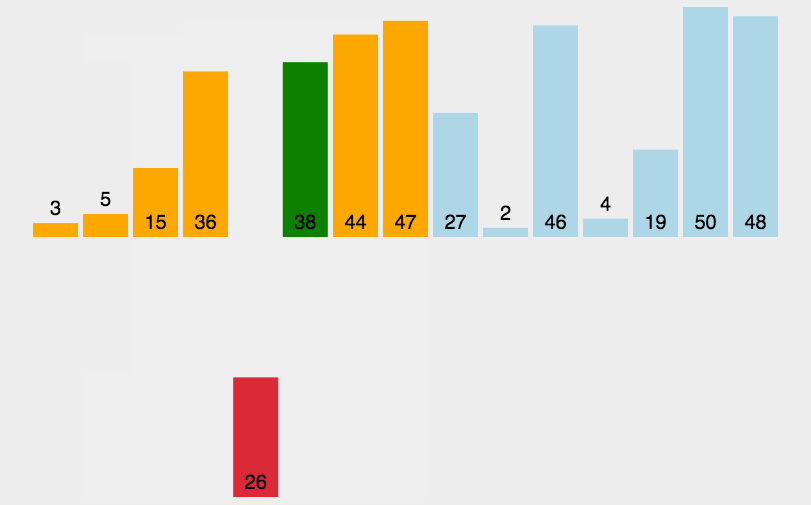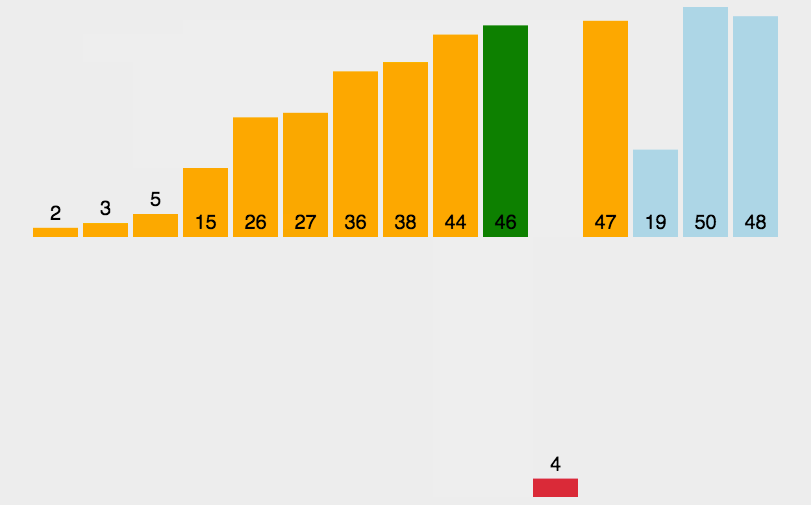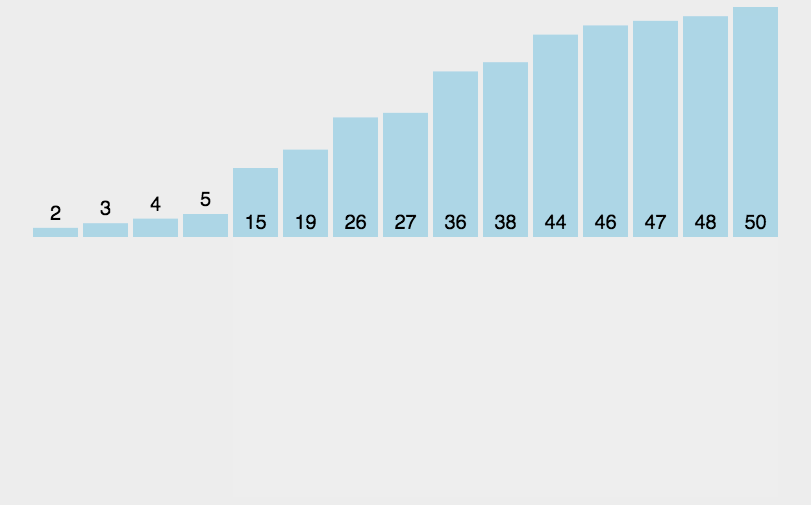
代码实现:
插入排序代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14function insertSort(arr) {
for (var i = 1; i < arr.length; i++) {
var insertVal = arr[i];
for (var j = i-1; j >= 0; j--) {
if (arr[j] > insertVal) {
arr[j+1] = arr[j];
} else {
break;
}
}
arr[j+1] = insertVal;
}
return arr;
}
3.4 归并排序(递归、合并)
基本原理:
创建在归并操作上的一种有效的排序算法,效率为 {\displaystyle O(n\log n)} {\displaystyle O(n\log n)}(大O符号)。1945年由约翰·冯·诺伊曼首次提出。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用,且各层分治递归可以同时进行。
排序步骤:
1.不断将数组对半分,直到每个数组只有一个;
2.将分出来的部分重新合并;
3.合并的时候按顺序排列。
图像展示:
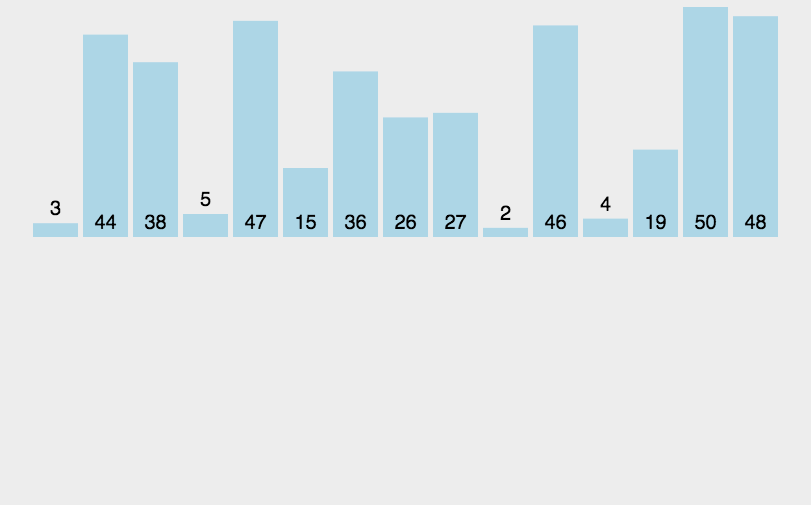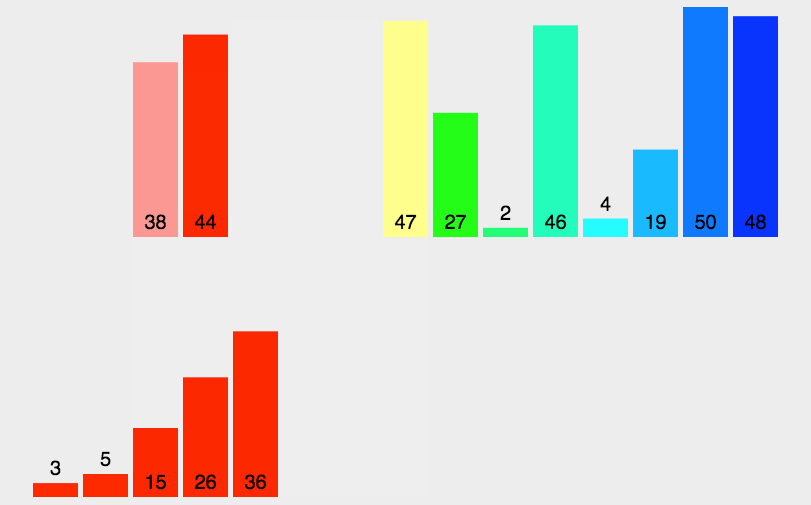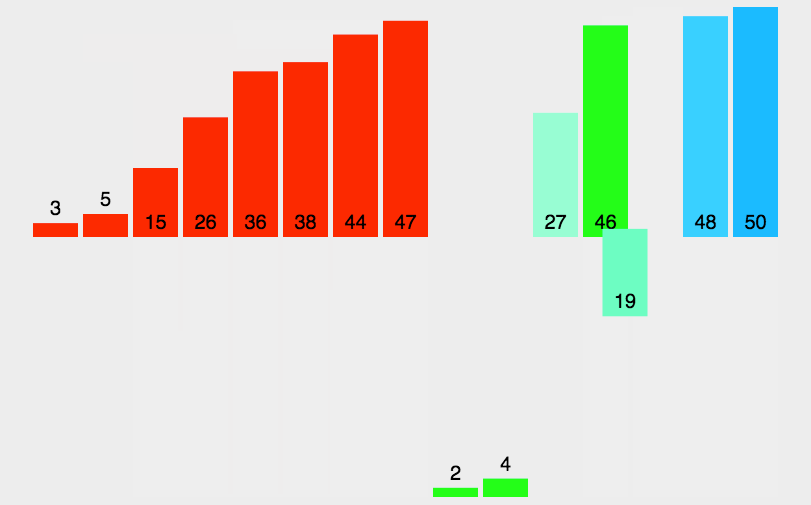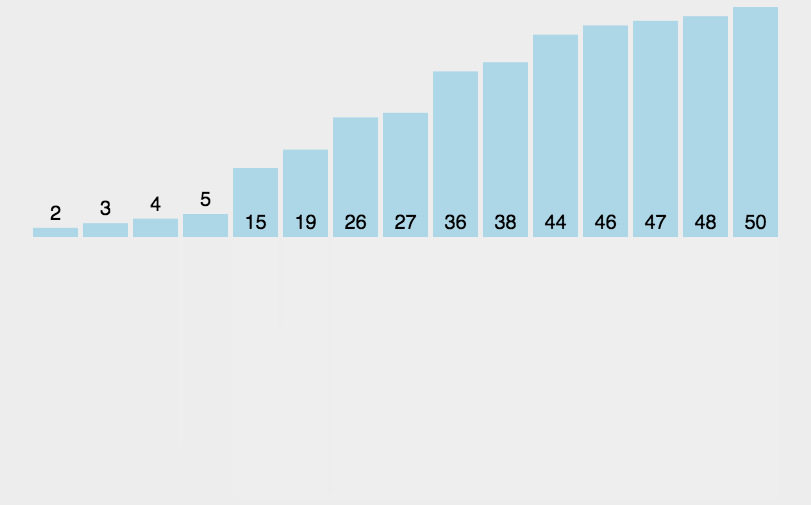
代码实现:
合并排序代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29function mergeSort(arr) {
var len = arr.length;
if (len < 2) {
return arr;
}
var middle = Math.floor(len/2);
var left = arr.slice(0, middle);
var right = arr.slice(middle);
return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right) {
var result = [];
while (left.length && right.length) {
if (left[0] <= right[0]) {
result.push(left.shift());
} else {
result.push(right.shift());
}
}
while (left.length) {
result.push(left.shift());
}
while (right.length) {
result.push(right.shift());
}
return result;
}
3.5 快速排序
基本原理:
使用分治法(Divide and conquer)策略来把一个序列(list)分为两个子序列(sub-lists)。
排序步骤:
1.以一个数为基准(第一个数),比基准小的放到左边,比基准大的放到右边;
2.再按此方法对这两部分数据分别进行快速排序(递归进行);
3.不能再分后退出递归,并重新将数组合并。
图像展示:
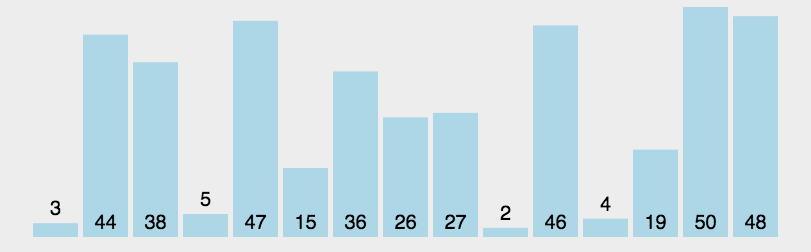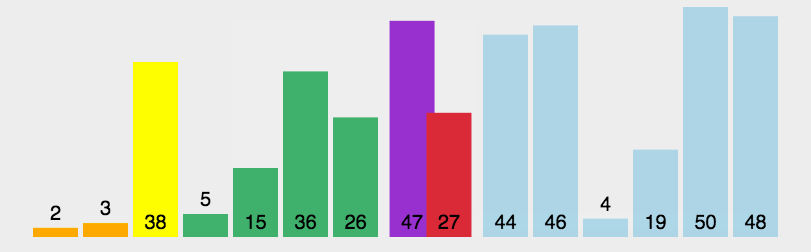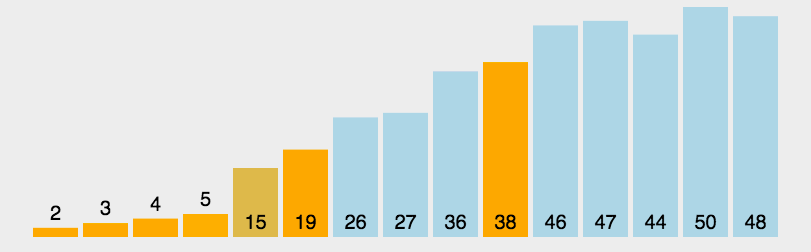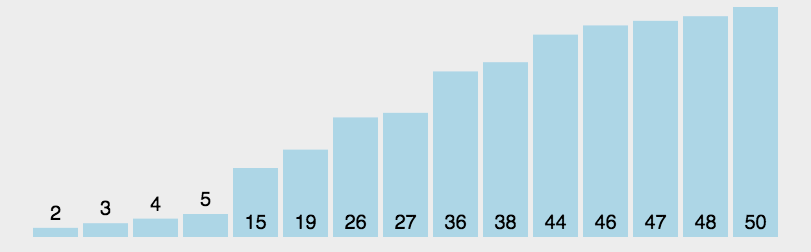
代码实现:
快速排序代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15function quickSort(arr) {
var len = arr.length;
if (len < 2) {
return arr;
}
var middleVal = arr[0], left = [], right = [];
for (var i = 1; i < len; i++) {
if (arr[i] <= middleVal) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return quickSort(left).concat([middleVal], quickSort(right));
}